TensorFlow基础¶
本章介绍TensorFlow的基本操作。
前置知识:
- Python基本操作 (赋值、分支及循环语句、使用import导入库);
- Python的With语句 ;
- NumPy ,Python下常用的科学计算库。TensorFlow与之结合紧密;
- 向量 和 矩阵 运算(矩阵的加减法、矩阵与向量相乘、矩阵与矩阵相乘、矩阵的转置等。测试题:
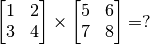 );
); - 函数的导数 ,多元函数求导 (测试题:
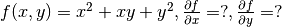 );
); - 线性回归 ;
- 梯度下降方法 求函数的局部最小值。
TensorFlow 1+1¶
我们可以先简单地将TensorFlow视为一个科学计算库(类似于Python下的NumPy)。这里以计算 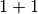 和
和 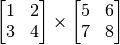 作为Hello World的示例。
作为Hello World的示例。
import tensorflow as tf
tf.enable_eager_execution()
a = tf.constant(1)
b = tf.constant(1)
c = tf.add(a, b) # 也可以直接写 c = a + b,两者等价
print(c)
A = tf.constant([[1, 2], [3, 4]])
B = tf.constant([[5, 6], [7, 8]])
C = tf.matmul(A, B)
print(C)
输出:
tf.Tensor(2, shape=(), dtype=int32)
tf.Tensor(
[[19 22]
[43 50]], shape=(2, 2), dtype=int32)
以上代码声明了 a、b、A、B 四个 张量 (Tensor),并使用了 tf.add() 和 tf.matmul() 两个 操作 (Operation)对张量进行了加法和矩阵乘法运算,运算结果即时存储于 c、C 两个张量内。张量的重要属性是其形状(shape)和类型(dtype)。这里 a、b、c 是纯量,形状为空,类型为int32;A、B、C 为2×2的矩阵,形状为 (2, 2),类型为int32。
在机器学习中,我们经常需要计算函数的导数。TensorFlow提供了强大的 自动求导机制 来计算导数。以下代码展示了如何使用 tf.GradientTape() 计算函数 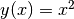 在
在 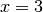 时的导数:
时的导数:
import tensorflow as tf
tf.enable_eager_execution()
x = tf.get_variable('x', shape=[1], initializer=tf.constant_initializer(3.))
with tf.GradientTape() as tape: # 在 tf.GradientTape() 的上下文内,所有计算步骤都会被记录以用于求导
y = tf.square(x)
y_grad = tape.gradient(y, x) # 计算y关于x的导数
print([y.numpy(), y_grad.numpy()])
输出:
[array([9.], dtype=float32), array([6.], dtype=float32)]
这里 x 是一个初始化为3的 变量 (Variable),使用 tf.get_variable() 声明。与普通张量一样,变量同样具有形状(shape)和类型(dtype)属性,不过使用变量需要有一个初始化过程,可以通过在 tf.get_variable() 中指定 initializer 参数来指定所使用的初始化器。这里使用 tf.constant_initializer(3.) 将变量 x 初始化为float32类型的 3. [1]。变量与普通张量的一个重要区别是其默认能够被TensorFlow的自动求导机制所求导,因此往往被用于定义机器学习模型的参数。 tf.GradientTape() 是一个自动求导的记录器,在其中的变量和计算步骤都会被自动记录。上面的示例中,变量 x 和计算步骤 y = tf.square(x) 被自动记录,因此可以通过 y_grad = tape.gradient(y, x) 求张量 y 对变量 x 的导数。
在机器学习中,更加常见的是对多元函数求偏导数,以及对向量或矩阵的求导。这些对于TensorFlow也不在话下。以下代码展示了如何使用 tf.GradientTape() 计算函数 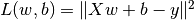 在
在 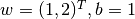 时分别对
时分别对 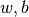 的偏导数。其中
的偏导数。其中 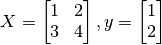 。
。
X = tf.constant([[1., 2.], [3., 4.]])
y = tf.constant([[1.], [2.]])
w = tf.get_variable('w', shape=[2, 1], initializer=tf.constant_initializer([[1.], [2.]]))
b = tf.get_variable('b', shape=[1], initializer=tf.constant_initializer([1.]))
with tf.GradientTape() as tape:
L = 0.5 * tf.reduce_sum(tf.square(tf.matmul(X, w) + b - y))
w_grad, b_grad = tape.gradient(L, [w, b]) # 计算L(w, b)关于w, b的偏导数
print([L.numpy(), w_grad.numpy(), b_grad.numpy()])
输出:
[62.5, array([[35.],
[50.]], dtype=float32), array([15.], dtype=float32)]
这里, tf.square() 操作代表对输入张量的每一个元素求平方,不改变张量形状。 tf.reduce_sum() 操作代表对输入张量的所有元素求和,输出一个形状为空的纯量张量(可以通过 axis 参数来指定求和的维度,不指定则默认对所有元素求和)。TensorFlow中有大量的张量操作API,包括数学运算、张量形状操作(如 tf.reshape())、切片和连接(如 tf.concat())等多种类型,可以通过查阅TensorFlow的官方API文档 [2] 来进一步了解。
从输出可见,TensorFlow帮助我们计算出了
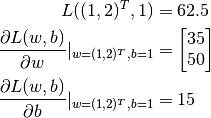
基础示例:线性回归¶
考虑一个实际问题,某城市在2013年-2017年的房价如下表所示:
| 年份 | 2013 | 2014 | 2015 | 2016 | 2017 |
| 房价 | 12000 | 14000 | 15000 | 16500 | 17500 |
现在,我们希望通过对该数据进行线性回归,即使用线性模型 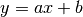 来拟合上述数据,此处
来拟合上述数据,此处 a 和 b 是待求的参数。
首先,我们定义数据,进行基本的归一化操作。
import numpy as np
X_raw = np.array([2013, 2014, 2015, 2016, 2017], dtype=np.float32)
y_raw = np.array([12000, 14000, 15000, 16500, 17500], dtype=np.float32)
X = (X_raw - X_raw.min()) / (X_raw.max() - X_raw.min())
y = (y_raw - y_raw.min()) / (y_raw.max() - y_raw.min())
接下来,我们使用梯度下降方法来求线性模型中两个参数 a 和 b 的值 [3]。
回顾机器学习的基础知识,对于多元函数 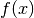 求局部极小值,梯度下降 的过程如下:
求局部极小值,梯度下降 的过程如下:
初始化自变量为
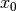 ,
, 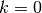
迭代进行下列步骤直到满足收敛条件:
- 求函数
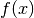 关于自变量的梯度
关于自变量的梯度 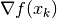
- 更新自变量:
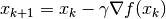 。这里
。这里 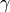 是学习率(也就是梯度下降一次迈出的“步子”大小)
是学习率(也就是梯度下降一次迈出的“步子”大小) 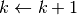
- 求函数
接下来,我们考虑如何使用程序来实现梯度下降方法,求得线性回归的解 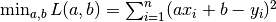 。
。
NumPy¶
机器学习模型的实现并不是TensorFlow的专利。事实上,对于简单的模型,即使使用常规的科学计算库或者工具也可以求解。在这里,我们使用NumPy这一通用的科学计算库来实现梯度下降方法。NumPy提供了多维数组支持,可以表示向量、矩阵以及更高维的张量。同时,也提供了大量支持在多维数组上进行操作的函数(比如下面的 np.dot() 是求内积, np.sum() 是求和)。在这方面,NumPy和MATLAB比较类似。在以下代码中,我们手工求损失函数关于参数 a 和 b 的偏导数 [4],并使用梯度下降法反复迭代,最终获得 a 和 b 的值。
a, b = 0, 0
num_epoch = 10000
learning_rate = 1e-3
for e in range(num_epoch):
# 手动计算损失函数关于自变量(模型参数)的梯度
y_pred = a * X + b
grad_a, grad_b = (y_pred - y).dot(X), (y_pred - y).sum()
# 更新参数
a, b = a - learning_rate * grad_a, b - learning_rate * grad_b
print(a, b)
然而,你或许已经可以注意到,使用常规的科学计算库实现机器学习模型有两个痛点:
- 经常需要手工求函数关于参数的偏导数。如果是简单的函数或许还好,但一旦函数的形式变得复杂(尤其是深度学习模型),手工求导的过程将变得非常痛苦,甚至不可行。
- 经常需要手工根据求导的结果更新参数。这里使用了最基础的梯度下降方法,因此参数的更新还较为容易。但如果使用更加复杂的参数更新方法(例如Adam或者Adagrad),这个更新过程的编写同样会非常繁杂。
而TensorFlow等深度学习框架的出现很大程度上解决了这些痛点,为机器学习模型的实现带来了很大的便利。
TensorFlow¶
TensorFlow的 Eager Execution(动态图)模式 [5] 与上述NumPy的运行方式十分类似,然而提供了更快速的运算(GPU支持)、自动求导、优化器等一系列对深度学习非常重要的功能。以下展示了如何使用TensorFlow计算线性回归。可以注意到,程序的结构和前述NumPy的实现非常类似。这里,TensorFlow帮助我们做了两件重要的工作:
- 使用
tape.gradient(ys, xs)自动计算梯度; - 使用
optimizer.apply_gradients(grads_and_vars)自动更新模型参数。
X = tf.constant(X)
y = tf.constant(y)
a = tf.get_variable('a', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
b = tf.get_variable('b', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
variables = [a, b]
num_epoch = 10000
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-3)
for e in range(num_epoch):
# 使用tf.GradientTape()记录损失函数的梯度信息
with tf.GradientTape() as tape:
y_pred = a * X + b
loss = 0.5 * tf.reduce_sum(tf.square(y_pred - y))
# TensorFlow自动计算损失函数关于自变量(模型参数)的梯度
grads = tape.gradient(loss, variables)
# TensorFlow自动根据梯度更新参数
optimizer.apply_gradients(grads_and_vars=zip(grads, variables))
在这里,我们使用了前文的方式计算了损失函数关于参数的偏导数。同时,使用 tf.train.GradientDescentOptimizer(learning_rate=1e-3) 声明了一个梯度下降 优化器 (Optimizer),其学习率为1e-3。优化器可以帮助我们根据计算出的求导结果更新模型参数,从而最小化某个特定的损失函数,具体使用方式是调用其 apply_gradients() 方法。
注意到这里,更新模型参数的方法 optimizer.apply_gradients() 需要提供参数 grads_and_vars,即待更新的变量(如上述代码中的 variables )及损失函数关于这些变量的偏导数(如上述代码中的 grads )。具体而言,这里需要传入一个Python列表(List),列表中的每个元素是一个(变量的偏导数,变量)对。比如这里是 [(grad_w, w), (grad_b, b)] 。我们通过 grads = tape.gradient(loss, variables) 求出tape中记录的 loss 关于 variables = [w, b] 中每个变量的偏导数,也就是 grads = [grad_w, grad_b],再使用Python的 zip() 函数将 grads = [grad_w, grad_b] 和 vars = [w, b] 拼装在一起,就可以组合出所需的参数了。
在实际应用中,我们编写的模型往往比这里一行就能写完的线性模型 y_pred = tf.matmul(X, w) + b 要复杂得多。所以,我们往往会编写一个模型类,然后在需要调用的时候使用 y_pred = model(X) 进行调用。关于模型类的编写方式可见 下章。
| [1] | Python中可以使用整数后加小数点表示将该整数定义为浮点数类型。例如 3. 代表浮点数 3.0。 |
| [2] | 主要可以参考 Tensor Transformations 和 Math 两个页面。可以注意到,TensorFlow的张量操作API在形式上和Python下流行的科学计算库NumPy非常类似,如果对后者有所了解的话可以快速上手。 |
| [3] | 其实线性回归是有解析解的。这里使用梯度下降方法只是为了展示TensorFlow的运作方式。 |
| [4] | 此处的损失函数为均方差 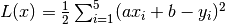 。其关于参数 。其关于参数 a 和 b 的偏导数为 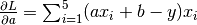 , ,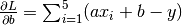 |
| [5] | 与Eager Execution相对的是Graph Execution(静态图)模式,即TensorFlow在2018年3月的1.8版本发布之前所主要使用的模式。本手册以面向快速迭代开发的动态模式为主,但会在附录中介绍静态图模式的基本使用,供需要的读者查阅。 |