附录：静态的TensorFlow

TensorFlow 1+1

TensorFlow本质上是一个符号式的（基于计算图的）计算框架。这里以计算1+1作为Hello World的示例。

import tensorflow as tf

# 定义一个“计算图”
a = tf.constant(1)  # 定义一个常量Tensor（张量）
b = tf.constant(1)
c = a + b  # 等价于 c = tf.add(a, b)，c是张量a和张量b通过Add这一Operation（操作）所形成的新张量

sess = tf.Session()     # 实例化一个Session（会话）
c_ = sess.run(c)        # 通过Session的run()方法对计算图里的节点（张量）进行实际的计算
print(c_)

输出:

2

上面这个程序只能计算1+1，以下程序通过 tf.placeholder() （占位符张量）和 sess.run() 的 feed_dict= 参数展示了如何使用TensorFlow计算任意两个数的和：

import tensorflow as tf

a = tf.placeholder(dtype=tf.int32)  # 定义一个占位符Tensor
b = tf.placeholder(dtype=tf.int32)
c = a + b

a_ = input("a = ")  # 从终端读入一个整数并放入变量a_
b_ = input("b = ")

sess = tf.Session()
c_ = sess.run(c, feed_dict={a: a_, b: b_})  # feed_dict参数传入为了计算c所需要的张量的值
print("a + b = %d" % c_)

运行程序:

>>> a = 2
>>> b = 3
a + b = 5

**变量**（Variable）是一种特殊类型的张量，使用 tf.get_variable() 建立，与编程语言中的变量很相似。使用变量前需要先初始化，变量内存储的值可以在计算图的计算过程中被修改。以下示例如何建立一个变量，将其值初始化为0，并逐次累加1。

import tensorflow as tf

a = tf.get_variable(name='a', shape=[])
initializer = tf.assign(a, 0)   # tf.assign(x, y)返回一个“将张量y的值赋给变量x”的操作
a_plus_1 = a + 1    # 等价于 a + tf.constant(1)
plus_one_op = tf.assign(a, a_plus_1)

sess = tf.Session()
sess.run(initializer)
for i in range(5):
    sess.run(plus_one_op)                   # 对变量a执行加一操作
    a_ = sess.run(a)                        # 获得变量a的值并存入a_
    print(a_)

输出:

1.0
2.0
3.0
4.0
5.0

以下代码和上述代码等价，在声明变量时指定初始化器，并通过 tf.global_variables_initializer() 一次性初始化所有变量，在实际工程中更常用：

import tensorflow as tf

a = tf.get_variable(name='a', shape=[], initializer=tf.zeros_initializer)   # 指定初始化器为全0初始化
a_plus_1 = a + 1
plus_one_op = tf.assign(a, a_plus_1)

sess = tf.Session()
sess.run(tf.global_variables_initializer()) # 初始化所有变量
for i in range(5):
    sess.run(plus_one_op)
    a_ = sess.run(a)
    print(a_)

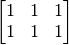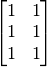矩阵乃至张量运算是科学计算（包括机器学习）的基本操作。以下程序展示如何计算两个矩阵 和 的乘积：

import tensorflow as tf

A = tf.ones(shape=[2, 3])   # tf.ones(shape)定义了一个形状为shape的全1矩阵
B = tf.ones(shape=[3, 2])
C = tf.matmul(A, B)

sess = tf.Session()
C_ = sess.run(C)
print(C_)

输出:

[[3. 3.]
 [3. 3.]]

Placeholder（占位符张量）和Variable（变量张量）也同样可以为向量、矩阵乃至更高维的张量。

基础示例：线性回归

与前面的NumPy和Eager Execution模式不同，TensorFlow的Graph Execution模式使用 符号式编程 来进行数值运算。首先，我们需要将待计算的过程抽象为数据流图，将输入、运算和输出都用符号化的节点来表达。然后，我们将数据不断地送入输入节点，让数据沿着数据流图进行计算和流动，最终到达我们需要的特定输出节点。以下代码展示了如何基于TensorFlow的符号式编程方法完成与前节相同的任务。其中， tf.placeholder() 即可以视为一种“符号化的输入节点”，使用 tf.get_variable() 定义模型的参数（Variable类型的张量可以使用 tf.assign() 进行赋值），而 sess.run(output_node, feed_dict={input_node: data}) 可以视作将数据送入输入节点，沿着数据流图计算并到达输出节点并返回值的过程。

import tensorflow as tf

# 定义数据流图
learning_rate_ = tf.placeholder(dtype=tf.float32)
X_ = tf.placeholder(dtype=tf.float32, shape=[5])
y_ = tf.placeholder(dtype=tf.float32, shape=[5])
a = tf.get_variable('a', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
b = tf.get_variable('b', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)

y_pred = a * X_ + b
loss = tf.constant(0.5) * tf.reduce_sum(tf.square(y_pred - y_))

# 反向传播，手动计算变量（模型参数）的梯度
grad_a = tf.reduce_sum((y_pred - y_) * X_)
grad_b = tf.reduce_sum(y_pred - y_)

# 梯度下降法，手动更新参数
new_a = a - learning_rate_ * grad_a
new_b = b - learning_rate_ * grad_b
update_a = tf.assign(a, new_a)
update_b = tf.assign(b, new_b)

train_op = [update_a, update_b] 
# 数据流图定义到此结束
# 注意，直到目前，我们都没有进行任何实质的数据计算，仅仅是定义了一个数据图

num_epoch = 10000
learning_rate = 1e-3
with tf.Session() as sess:
    # 初始化变量a和b
    tf.global_variables_initializer().run()
    # 循环将数据送入上面建立的数据流图中进行计算和更新变量
    for e in range(num_epoch):
        sess.run(train_op, feed_dict={X_: X, y_: y, learning_rate_: learning_rate})
    print(sess.run([a, b]))

在上面的两个示例中，我们都是手工计算获得损失函数关于各参数的偏导数。但当模型和损失函数都变得十分复杂时（尤其是深度学习模型），这种手动求导的工程量就难以接受了。TensorFlow提供了 自动求导机制 ，免去了手工计算导数的繁琐。利用TensorFlow的求导函数 tf.gradients(ys, xs) 求出损失函数loss关于a，b的偏导数。由此，我们可以将上节中的两行手工计算导数的代码

# 反向传播，手动计算变量（模型参数）的梯度
grad_a = tf.reduce_sum((y_pred - y_) * X_)
grad_b = tf.reduce_sum(y_pred - y_)

替换为

grad_a, grad_b = tf.gradients(loss, [a, b])

计算结果将不会改变。

甚至不仅于此，TensorFlow附带有多种 优化器 （optimizer），可以将求导和梯度更新一并完成。我们可以将上节的代码

# 反向传播，手动计算变量（模型参数）的梯度
grad_a = tf.reduce_sum((y_pred - y_) * X_)
grad_b = tf.reduce_sum(y_pred - y_)

# 梯度下降法，手动更新参数
new_a = a - learning_rate_ * grad_a
new_b = b - learning_rate_ * grad_b
update_a = tf.assign(a, new_a)
update_b = tf.assign(b, new_b)

train_op = [update_a, update_b] 

整体替换为

optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate_)
grad = optimizer.compute_gradients(loss)
train_op = optimizer.apply_gradients(grad)

这里，我们先实例化了一个TensorFlow中的梯度下降优化器 tf.train.GradientDescentOptimizer() 并设置学习率。然后利用其 compute_gradients(loss) 方法求出 loss 对所有变量（参数）的梯度。最后通过 apply_gradients(grad) 方法，根据前面算出的梯度来梯度下降更新变量（参数）。

以上三行代码等价于下面一行代码：

train_op = tf.train.GradientDescentOptimizer(learning_rate=learning_rate_).minimize(loss)

简化后的代码如下：

import tensorflow as tf

learning_rate_ = tf.placeholder(dtype=tf.float32)
X_ = tf.placeholder(dtype=tf.float32, shape=[5])
y_ = tf.placeholder(dtype=tf.float32, shape=[5])
a = tf.get_variable('a', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
b = tf.get_variable('b', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)

y_pred = a * X_ + b
loss = tf.constant(0.5) * tf.reduce_sum(tf.square(y_pred - y_))

# 反向传播，利用TensorFlow的梯度下降优化器自动计算并更新变量（模型参数）的梯度
train_op = tf.train.GradientDescentOptimizer(learning_rate=learning_rate_).minimize(loss)

num_epoch = 10000
learning_rate = 1e-3
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for e in range(num_epoch):
        sess.run(train_op, feed_dict={X_: X, y_: y, learning_rate_: learning_rate})
    print(sess.run([a, b]))